Doubling Your Money

One of my first real articles was about the Rule of 72 (more Einstein Finance). The Rule of 72 is a simple heuristic for figuring out when your money can double in value, given a specific (compounding) growth rate.

Let’s make sure we are clear: the model I am working from assumes:

• I am putting an amount into a savings vehicle and not adding any more (so the model is flawed already but stay with me on this)
• The rate of return stays the same throughout the period (again flawed)

When I say doubling, based on those assumptions, it is when the initial investment is now worth twice what it was initially.

I attempted to clarify my initial post with a very grainy-looking graph in Einstein: The Rule of 72 a few years later, but I think we can do better than that now.

First a simple table following the formula:

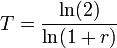
Where T is the number of period and r is the interest rate compounded in that period, and the ln() function is the Natural Log (mascot of the University of Waterloo MathSoc).

---

---

Rate (r)	Period to Double (T) in years
0.50%	139.0
1.00%	69.7
1.50%	46.6
2.00%	35.0
2.50%	28.1
3.00%	23.4
3.50%	20.1
4.00%	17.7
4.50%	15.7
5.00%	14.2
5.50%	12.9
6.00%	11.9
6.50%	11.0
7.00%	10.2
7.50%	9.6
8.00%	9.0
8.50%	8.5
9.00%	8.0
9.50%	7.6
10.00%	7.3
10.50%	6.9
11.00%	6.6
11.50%	6.4
12.00%	6.1
12.50%	5.9
13.00%	5.7
13.50%	5.5
14.00%	5.3
14.50%	5.1
15.00%	5.0

Simple calculation, isn’t it? You can see that it doesn’t take long to go from taking 135 years to double your investment to 15 years to double your investment (0.5% to 4.5%), but it is easier to see in a graph how this all works:

This is a straightforward model, given very few folks dump a load of money into a single investment and let it grow with no intervention. Still, it is worthwhile to understand that when someone talks about getting a 4.0% growth on their investment, that means their investment will double in 18 years (or so). It is a handy model to remember.